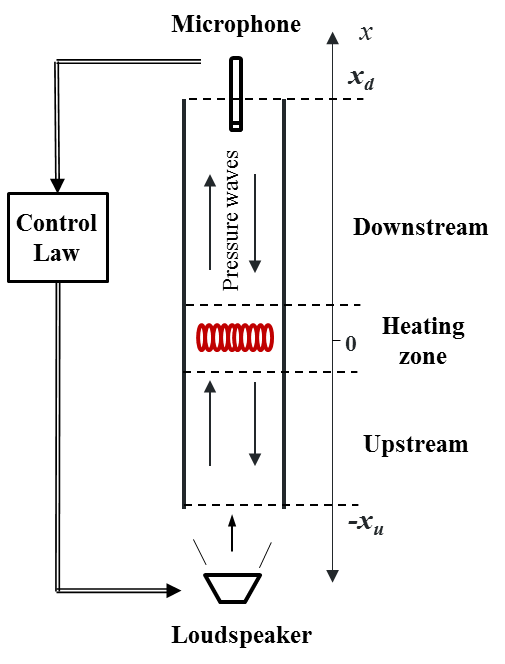
The image on the left shows a typical Rijke tube setup with a control system in the loop. Our experimental setup in the laboratory is on the right.
ANALYTICAL PREDICTION OF INSTABILITY USING THE CTCR PARADIGM
Below are some videos demonstrating our work regarding the analytical prediction of thermoacoustic instability and some experimental verifications.
For more info about this study, see the following papers:
“Predicting Thermoacoustic Instability: A Novel Analytical Approach and Its Experimental Validation”, (N. Olgac, U. Zalluhoglu, A. S. Kammer), Journal of Propulsion and Power, 30 (4), pp. 1005-1015, 2014.
“Parametric Investigation of Thermoacoustic Instability (TAI) in a Rijke tube: A Time-delay Perspective”, (N. Olgac, R. Cepeda-Gomez, U. Zalluhoglu, A. S. Kammer), International Journal of Spray and Combustion Dynamics, 7 (1), pp. 39-68, 2015.
|
The stability chart shown in the upper-left pane is generated via the CTCR paradigm. The x and y axes are upstream and downstream tube lengths, respectively. Notice that the diagonal line represents a constant tube length, which is in this case 48 inches (xu + xd = 48 in). Green dots on this diagonal line are points for which instability was also observed experimentally. Notice that perfect correspondence exist in the lower half of the tube. The upper-right pane shows characteristic roots as numerically calculated via the QPmR algorithm. The bottom-left pane displays sound pressure in the tube recorded via a piezo-microphone. In the bottom-right corner, the frequency distribution of the recorded pressure signal is shown. |
|
This video shows an experimental test run. The heating element is slowly pulled upwards starting from near the bottom end of the tube. Notice how the tube starts humming as the heat source traverses through unstable regions predicted by the CTCR stability charts of the previous video. The sound pressure waves are observed on the oscilloscope. |
FEEDBACK CONTROL OF THERMOACOUSTIC INSTABILITY
Below is a video demonstrating our work regarding the feedback control of thermoacoustic instability and some experimental verifications.
For more info about this study, see the following papers:
“A new perspective in designing delayed feedback control for thermoacoustic instabilities (TAI)”, (N. Olgac, U. Zalluhoglu, A. S. Kammer), Combustion Science and Technology, 187(5), pp. 697-720, 2015.
“Deployment of time delayed integral control for suppressing thermoacoustic instabilities”, (U. Zalluhoglu, N. Olgac), Journal of Guidance, Control and Dynamics (in press), 2016.
“Delayed feedback control laws for Rijke tube thermo-acoustic instability, synthesis and experimental validation”, (U. Zalluhoglu, A.S. Kammer, N. Olgac), IEEE Control Systems Technology (in press), 2016.
|
This video is on an experiment where we use a delayed feedback law to control thermoacoustic instability in a Rijke tube. The feedback control parameters (gain and delay) are synthesized analytically using the CTCR paradigm. For more information about this study, see our 2014 Combustion Science and Technology article which is currently in press. |
APPEARANCE OF SECONDARY-MODE INTERFERENCE IN THERMOACOUSTIC INSTABILITY OVER
PASSIVE (HELMHOLTZ RESONATOR) and ACTIVE CONTROLLED RIJKE TUBE
|
We demonstrate a common problem in the feedback control studies on thermoacoustic oscillations in a Rijke tube. When controller parameters are selected incorrectly, secondary (i.e., higher order) modes of the thermoacoustic dynamics may be destabilized, while the initially unstable mode is stabilized. Here, this event is analytically and experimentally studied over a Helmholtz-resonator-mounted Rijke tube (i.e., a passive absorber). The inappropriate controller parameter selections are revealed analytically using the Cluster Treatment of Characteristic Roots (CTCR) paradigm and the results are validated with experimental findings from a Rijke tube set-up. |